Теоретическая механика. Уравнения Лагранжа

В этой статье мы попробуем разобраться с такой темой, как "Уравнения Лагранжа". Вообще, уравнения Лагранжа довольно полезная штука, например, на их основе решаются задачи на малые колебания. В МГТУ им. Баумана в третьем семестре предлагается самостоятельное домашнее задание, в котором нужно записать уравнения Лагранжа для системы с двумя степенями свободы.

Итак, типовое задание выглядит так.

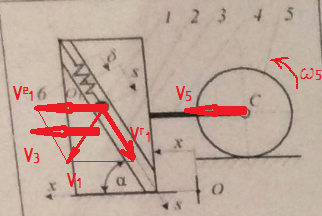
Прежде чем броситься решать эту задачу, посмотрим на задание и проанализируем его. Есть призма 3, которая движется поступательно по горизонтальной плоскости без трения. В призме сделан паз 2, по которому движется шарик 1. Если вы помните темы прошлого семестра, то легко увидите, что шарик совершает сложное движение - переносное поступательное вместе с призмой 3 и относительное поступательное по пазу 2. Далее есть стержень 4, который соединяет призму и каток 5. Очевидно, что скорость центра катка С равна скорость призмы. Каток движется без скольжения, это важный момент. Движение системы описывается двумя обобщенными координатами, которые любезно выбрал для нас составитель задания.

Итак, приступим к решению.

Поскольку обобщенных координат две (две степени свободы), система уравнений Лагранжа будет выглядеть так:

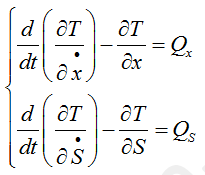Расчет начинаем с записи уравнений связи - выражаем скорости всех ключевых точек и тел, имеющих массу, через обобщенные координаты. Из сказанного ранее понятно, что нам понадобится линейная скорость призмы 3, линейная скорость катка 5, угловая скорость катка 5 и скорость шарика 1. С поступательным движением все просто

С угловой скоростью катка тоже все понятно. Так как проскальзывание отсутствует

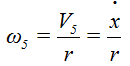
Самое трудное - выразить скорость шарика 1. Как мы уже говорили, он совершает сложное движение, значит, его скорость складывается из относительной и переносной. Переносная - это скорость поступательного движения призмы 3. Относительное - скольжение вдоль паза 2, которое описано координатой S. Значит

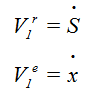
Векторно складываем эти две скорости

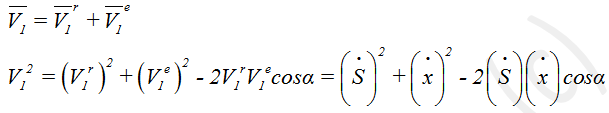
Второе выражение здесь - это теорема косинусов. Если нанести все векторы на рисунок, станет понятно, почему так. 

Определившись со скоростями, записываем выражение для кинетической энергии системы Т. Полная кинетическая энергия складывается из кинетических энергий всех тел, обладающих массой. То есть в нашем случае, тел 1, 3, 5.

Шарик 1 обладает энергией

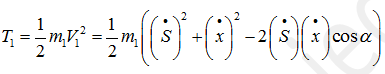
Призма 3 движется поступательно

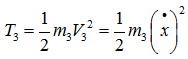
Каток 5 совершает плоское движение, так что его кинетическая энергия складывается из энергии поступательного и вращательного движений

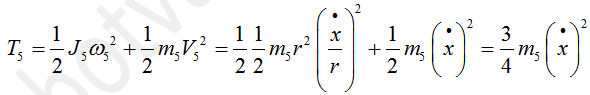
Полная кинетическая энергия системы

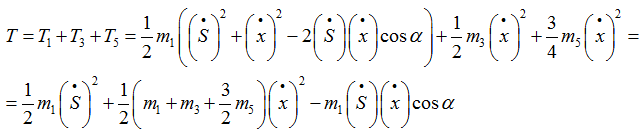
Для записи уравнений Лагранжа это выражение нужно несколько раз продифференцировать.

Сначала по координате x. Частные производные

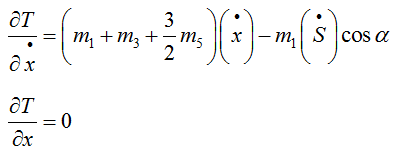
Производную по x с точкой дифференцируем по времени

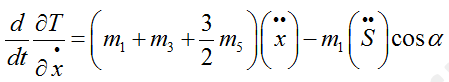
Теперь то же самое по координате S. Частные производные

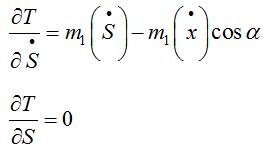
Производная по времени

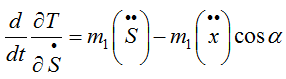
Левая часть уравнений Лагранжа готова. Займемся правой частью. Для нее нужно посчитать обобщенные силы по каждой координате. Есть несколько способов это сделать, мы предпочитаем делать это через элементарную работу на малом приращении координаты. В общем случае формула выглядит так

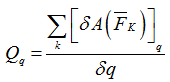
На практике это применяется следующим образом. Сначала нанесем на рисунок все действующие силы. В нашем случае это сила упругости пружины и силы тяжести.

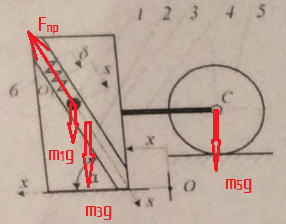
Сначала считаем обобщенную силу по координате x. Для этого мысленно "замораживаем" координату S, и позволяем системе свободно двигаться по координате x. То есть шарик "приклеивается" к пазу 2, и внутри него никуда не движется. Все перемещение происходит по координате x. Очевидно, что сила упругости работу не совершает, так как ее длина не меняется. Очевидно, что силы тяжести работу не совершают, так как движение происходит горизонтально. Официальным языком это записывается так

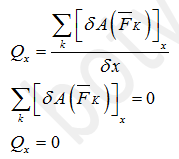
Теперь обобщенная сила по координате S. Мысленно "замораживаем" координату x. Получается, что призма 3 вместе с пазом 2 и катком 5 стоит на месте, а внутри неподвижного паза движется шарик. Сила упругости совершает работу, также как и сила тяжести шарика 1. Пружина была растянута на величину статической деформации δ и дополнительно растянута на S в произвольный момент времени, то есть сила упругости равна с·(δ+S). Работа силы упругости отрицательна, так как пружина растягивается. Работа силы тяжести шарика 1 положительна, так как шарик движется вниз. Силы тяжести призмы 3 и катка 5 работу не совершают, так как эти тела покоятся. Получаем

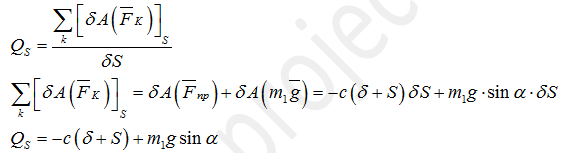
Собственно, все. Собираем все посчитанные величины в уравнения Лагранжа и получаем систему дифференциальных уравнений, описывающих движение системы.

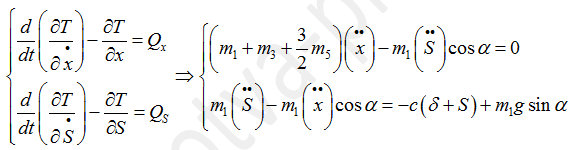
Для проверки можно посмотреть размерности, в обеих частях выражения размерности должны совпадать (обычно это ньютоны).

Конечно, разные задачи немного отличаются в ходе решения, но алгоритм всех задач примерно такой.

Подытожим:

1) Определить число степеней свободы и выбрать обобщенные координаты

2) Записать уравнения связей

3) Записать выражение для кинетической энергии

4) Взять необходимые производные

5) Записать обобщенные силы по каждой координате

6) Записать уравнения Лагранжа

Если что-то не получается, не отчаивайтесь, мы всегда рады помочь.

Всегда ваша, Botva-Project.