Теоретическая механика. Динамика точки.

Рассмотрим решение типовой задачи из домашнего задания по теоретической механике для 3-го семестра.

Условие

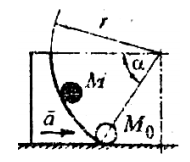Рабочая поверхность толкателя представляет собой цилиндрическую поверхность радиусом r с углом охвата α=45˚. Толкатель начинает двигаться по горизонтальной плоскости с постоянным ускорением а и приводит в движение тело, находящееся на плоскости в покое. Пренебрегая трением тела о поверхность толкателя, определить, при каком минимальном значении ускорения толкателя тело достигнет верхней кромки.

Решение

Если точка движется по окружности, имеет смысл задать ее положение угловой координатой. Определим положение точки М угловой координатой φ.

Перейдем в неинерциальную систему отсчета, связанную с движущимся толкателем. В соответствии с принципом Даламбера в системе отсчета, связанной с толкателем, на точку действует сила инерции:

Нанесем на рисунок все силы, действующие на точку. Это сила инерции (направлена в сторону, противоположную ускорению толкателя), сила нормальной реакции опоры (направлена нормально к опоре, т.е. в центр окружности), сила тяжести (направлена, разумеется, вниз).

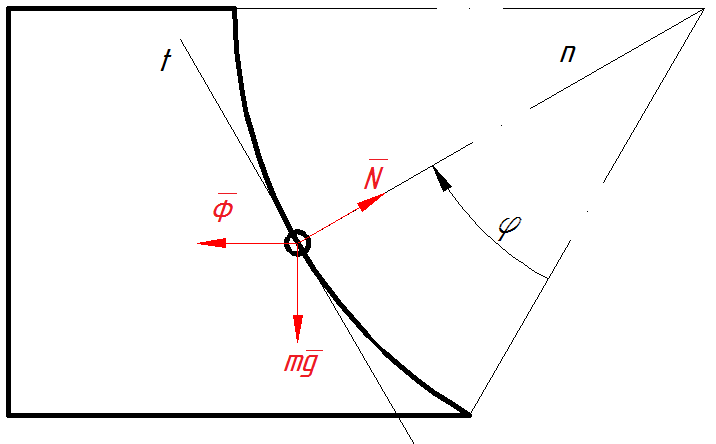
Векторное уравнение динамики точки выглядит так:

При данном выборе координат можно выделить две оси: ось t – касательную к траектории точки и ось n – нормальную к траектории точки. Наше векторное уравнение мы будем проецировать на эти оси.

В проекции на ось t:

Упрощаем выражение, используя тригонометрические тождества:

Запишем выражение для a_t, избавляясь от переменной t и выражая ускорение через угол φ

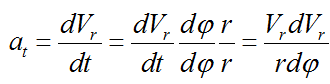
Переписываем выражение и получаем дифференциальное уравнение с разделяющимися переменными:

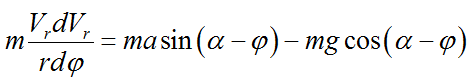
Сокращаем массу:

Интегрируем обе части уравнения. При выборе пределов интегрирования принимаем, что начальная скорость точки равна 0 (точка покоилась на плоскости), конечная скорость равна 0 (точка поднялась до верхней кромки толкателя и остановилась там). Угол φ меняется от 0 до α.

Получаем:

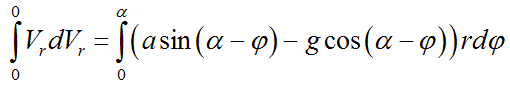
Интегрируем:

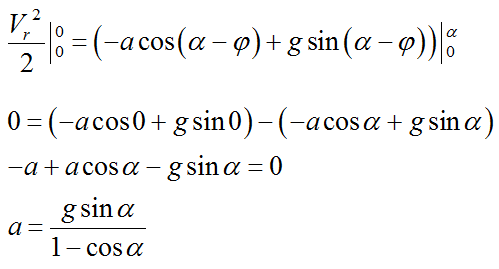
Полезно проверить размерность, хотя здесь она очевидна:

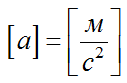
Подставим данные:

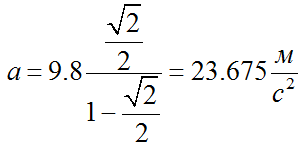
Как видим из ответа, ускорение толкателя не зависит от массы точки и от радиуса толкателя.

Подытожим. Вот общий алгоритм решения задач на динамику точки.

1)      Выбираем систему отсчета и задаем систему координат, однозначно описывающих положение точки

2)      Применяя принцип Даламбера, вводим силы инерции, если система отсчета не является инерциальной

3)      Наносим на рисунок все силы, действующие на точку, в некоем произвольном положении

4)      Записываем векторное уравнение равновесия точки (оно же уравнение динамики)

5)      Проецируем уравнение на оси таким образом, чтобы ненужные члены уравнения исчезли (как сила реакции N в нашем случае)

6)      Упрощаем то, что упрощается, получаем дифференциальное уравнение

7)      Решаем это уравнение, получаем ответ

8)      Проверяем размерность ответа и его логичность.

Если у Вас есть вопросы по решению данной задачи (или другой), пишите на наш e-mail botva-project@yandex.ru, мы всегда готовы помочь.

С уважением, Botva-Project